This post consists of two parts. The first part is aimed at introducing this new illusion to a general audience. The second part is intended to supplement technical details for specialist readers. Click here to navigate to the technical section of this post

Most people believe that what they see corresponds to reality, a philosophical position called “naive realism“.
This position is challenged by the existence of visual illusions, where perception differs from reality, revealing the subjective nature of our perception.
One such class of visual illusions is known as “illusory contours”. Presented with this illusion, observers perceive edges that are not actually there. The most well-known example of this phenomenon is the “Kanizsa triangle”.
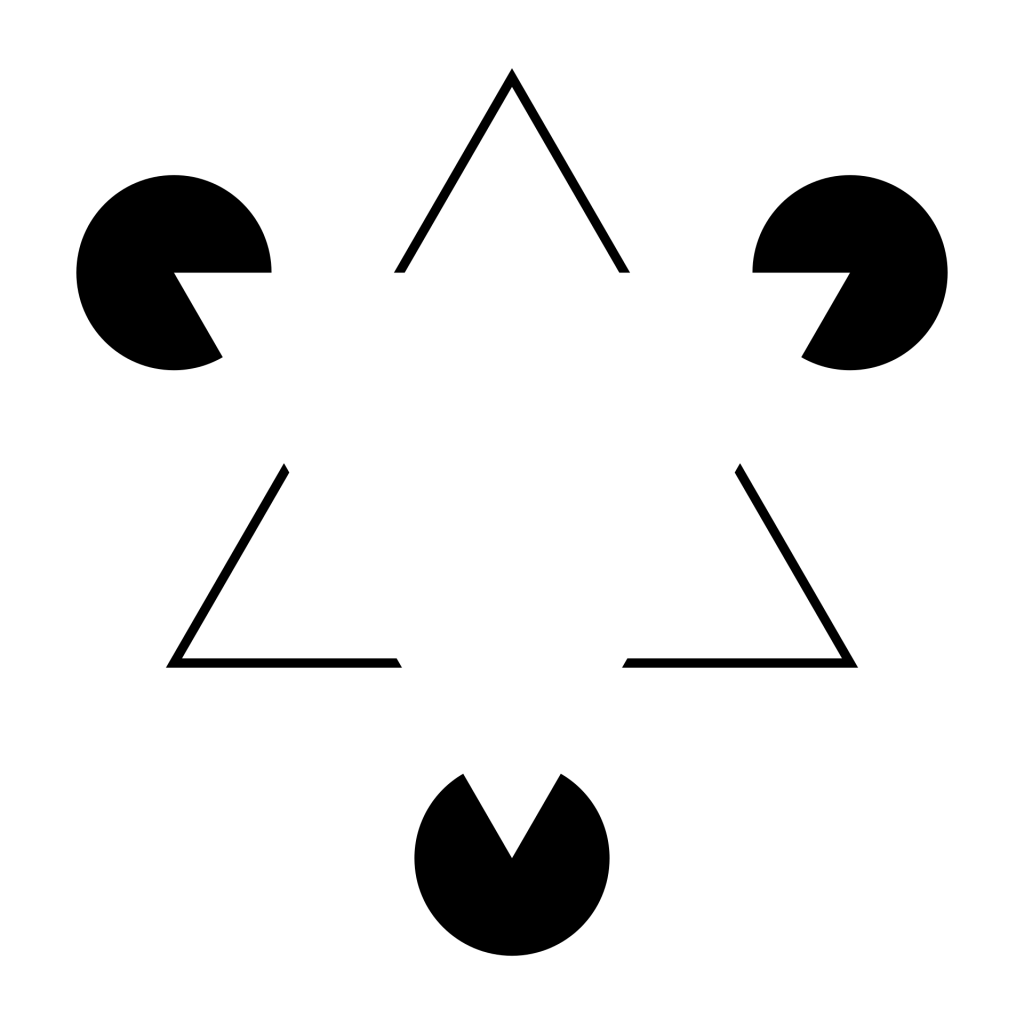
Most observers interpret this scene – assuming one is looking down from above – as a white triangle being on top of three black circles as well as another triangle, not as three pac-men and < ^ > symbols that just randomly happen to align in this configuration just by chance.
This illustrates another interesting principle of perception – there is compelling evidence that the brain favors the most likely (often the simplest) interpretation of a scene. In other words, the brain is routinely “connecting the dots” to fill in information that is not actually there, and has to do so, as not all necessary information is always fully available. These “best guesses” are often accurate, aiding in the survival of the organism.
All of this has been known for many decades.
In the image at the beginning of this post, bright – but fleeting – rays appear to emanate from the center of the image, akin to seeing the sun breaking through the clouds. Thus, we call this effect the “Scintillating Starburst“. However, these shimmering rays are entirely illusory: they’re the result of our brain connecting the dots. The starburst is not physically present.
What distinguishes this illusion from known effects is that in the Kanizsa triangle, the inducers (the pac-men) are luminance defined, whereas in our Scintillating Starburst, they are themselves the result of subtle features of our visual system.
Without getting too technical here (for details, see our paper), the Scintillating Starburst illusion can be explained as such: The black concentric “wreaths” (technically pairs of scaled star polygons) are all uniformly colored, but the part of our visual system that processes information from the periphery sees the intersection points as brighter than the rest of the wreath. As these “beacons” of brightness are aligned in linear fashion (along a ray projecting from the center), we believe the brain is connecting the dots accordingly, which is why most people see these illusory rays. What makes them shimmer or scintillate is the fact that another part of the visual system (that which processes information at the center of gaze) does not see the intersection points as brighter, but rather as they actually are. Thus, these rays will be fleeting due to the dynamic interplay between these two systems.
The phenomenology of this effect can be quite striking, and further enhanced by optimizing all stimulus dimensions (see paper) and by rotational motion.

Thus, the Scintillating Starburst is perhaps best understood as a “compound illusion” combining – and revealing – several features of our visual system, much like the “Lilac chaser”.
People readily interpret their environment in light of incomplete or unreliable information. For instance, when looking at stars, some observers are prone to see constellations. We believe the tendency of some people to “connect the dots” is related to their propensity to see non-existing ray patterns, for the same reason.
Note: This illusion was a finalist in the 2020 “best illusion of the year” contest.
Technical information and discussion
The purpose of this second part of the post is to address several technical points that did not make it into the paper itself (mostly because this was not the focus of the article, the reviewers asked us to take it out or it would have been too much of a tangent). Nevertheless, these points are important, so here we go.
One important consideration is the issue of “higher order” Starbursts (that are made up of star polygons with Schläfli numbers larger than the ones used in our study). For instance, Starbursts made up of bisecting star polygons (e.g. 14/2) are just a special case. n/3 starbursts trisect each other and still yield Scintillating Starbursts. Of course, such considerations open up a vast stimulus space. We are not claiming we found the most optimally possible Starburst (the one that evokes the strongest rays overall). The 14/2 Starburst is just the one we came across – serendipitously – first, so that is what we focused on in our empirical study.
This brings us to another consideration worth noting. To fully appreciate it, we first need to introduce some necessary terminology: A “wreath” consists of scaled pairs of Star Polygons such that they overlap. An “optimized wreath” consists of *scaled pairs* of Star Polygons that have minimal overlap. This is important because each Starburst has an optimal scale factor such that the star polygons just touch. When constructing Starbursts, one can either keep the scale factor and spacing between wreaths constant or vary it for each kind of star polygon. We decided to keep these factors constant (arguably a reasonable choice, given the vast potential space of stimulus dimensions), effectively optimizing all stimuli in our study to the 14/2 starburst, which is part of the reason why the 14/2 Starburst was perceived to evoke the strongest rays. It is possible that optimized 12/2 or 10/2 Starbursts could evoke rays with a similar strength as a 14/2, just fewer of them. Note that this consideration does not change any of our interpretations and conclusions of the paper. The point of this paper was to introduce the illusion and determine which – and how much – low-level visual attributes (such as contrast) contribute to the effect. Now that this has been determined, fully optimized starbursts can be explored properly.
This bring us to future directions. Four such directions seem obvious. One of them is – as mentioned – to determine which Starburst truly evokes the strongest effect – which is now feasible (doing this at the same time as the exploration of the low level features would have led to a combinatorial explosion, as the stimulus space is too large). See figure below for an appreciation of just how large this stimulus space is.
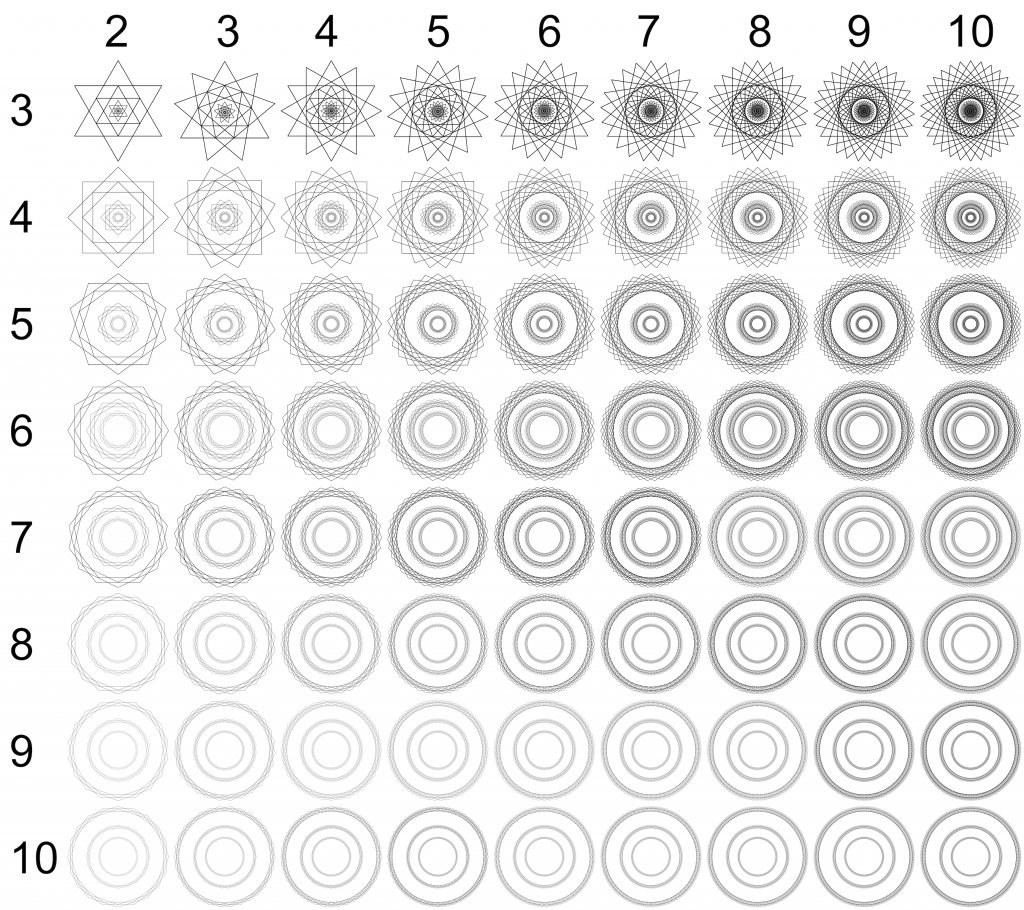
x-Axis: Turning number (of Schläfli notation).
y-axis: Number of sides of the base (convex) polygon
Some of the Starbursts in the first column – those in the first row (6/2), 3rd row (10/2) and 5th row (14/2) correspond to the types we used in our study
Second, we used subjective ratings as a dependent variable. Comparative judgment (2AFC) might be a better way to explore this effect psychophysically going forward, perhaps in conjunction with probing the underlying neurophysiology, which is the third point (our suggested mechanism – the dynamic interplay between foveal and peripheral vision is admittedly speculative at this point). Fourth – and finally – it would be interesting to link the propensity to see rays in the first place to personality characteristics. Not everyone sees constellations in the sky, just individual stars. Others cannot not see the constellations. It seems self-evident that there might be a differential propensity to connect the dots.
Finally, we would like to note an interesting observation which strengthens the conclusions we present here and in the paper. If the background is brighter than the shape, the illusory rays will appear brighter than the background. If the background is darker than the shape, the illusory rays will appear darker than the background. If background and shape are isoluminant, no rays appear (see figure below).

Note that nowhere in this account did we mention color. This seems to be strictly a story about luminance, not chromaticity. In other words, the mechanism we proposed above (and in the paper) is likely to be true – if there are “beacons”, rays emerge. If there are no beacons, there are no rays. The rays themselves are bright or dark, not colored. Taken together, we take this to suggest that our account – the interplay between the magnocellular system which creates the perception of the rays and the parvocellular system which doesn’t see them is likely to be correct.
To get a striking experience of how this is the case for a wide variety of color combinations and corresponding ray strengths, have a look at this video.
This brings us to a last point, namely similarity and differences to other, known effects. We have covered much of these already in the introduction to our paper, but this observation re color above (in addition to the considerations re Fourier Transform and luminance defined streaks we discuss in the paper) provides further evidence that we are dealing with a distinct phenomenon here:
As noted above, Scintillating Starbursts of any color yield either rays that are darker than the background, brighter than the background, or no rays. They do not yield colored rays. In contrast, the pincushion illusion does. Here, we made radial versions of the pincushion grids featured here. The illusory color is quite striking and clearly evident.



These color effects are undeniable. Moreover, these illusory lines or rays entirely static. They are not fleeting or scintillating. As Starbursts do not produce colored rays, but rays that scintillate, these are evidently different phenomena.
To conclude, we would like to note that the effect of induced scintillating rays is maximized if the line width of the wreaths that make up the Starburst stimulus scale with cortical magnification. Cortical magnification means that more real estate in the visual cortex is dedicated to central vision than to peripheral vision. So to make stimuli equally visible, they have to be scaled up, if they are presented in the periphery.


Just mental masturbation… Have a look at my 90s optical illusion: https://www.giannisarcone.com/wp/blog/2021/06/30/scintillating-starbust/
Thank you for your patience.
This statement is untrue. We carefully reviewed your published work and we found that – contrary to your claims – you do not mention illusory rays or scintillating starbursts anywhere until summer 2021, several days after the publication of our paper on this effect. So we would ask you to either provide evidence of your prior publication or desist from misrepresenting this issue.