Did a 6th century Hebrew fortuneteller accidentally do the first documented experiment?

Who did the first experiment? 13^th century scholastics like Roger Bacon are usually credited with the invention of the modern scientific method – in particular with regard to doing experiments. Bacon expanded on the work of Robert Grosseteste, who revived the method of induction and deduction from the ancients and applied it to the natural world (going far beyond Aristotle’s intuitive natural philosophy). Others give credit to even later individuals, such as another Bacon – Francis Bacon – who made the experiment the centerpiece of empirical investigations of the natural world.

However, it seems that the first experiment – admittedly with an ad hoc methodology and no clearly spelled out rationale linking outcomes and interpretation, let alone statistical considerations or power calculations – seems to have predated these developments by well over 600 years.

The backdrop to this experiment is straightforward – the Western Roman Empire fell in 476 to an onslaught of Goths, whereas the Eastern Roman Empire soldiered on. A bit more than 50 years later, the Eastern Roman Emperor (Justinian) tasked his General Belisarius to retake the lands of the Western Empire from the Goths, first and foremost the Italian peninsula.

Experimental design and outcome of what is potentially the first documented experiment.

The history of this conflict is relatively well documented, mostly by contemporary chroniclers like Procopius (in the pay of Justinian, so perhaps not entirely impartial). The story in question might be apocryphal and was already flagged as such by Procopius, but this does not really matter in this case – given that it is mostly the idea (of doing an experiment) itself that is of interest here, not its particular outcome. The story of the experiment is invoked to partially explain why Theodatus – the Gothic king in Rome, characterized by Procopius as “unmanly”, without experience in war and devoted to the pursuit of money – did not come to the aid of the denizens of Naples when they were besieged by Belisarius.

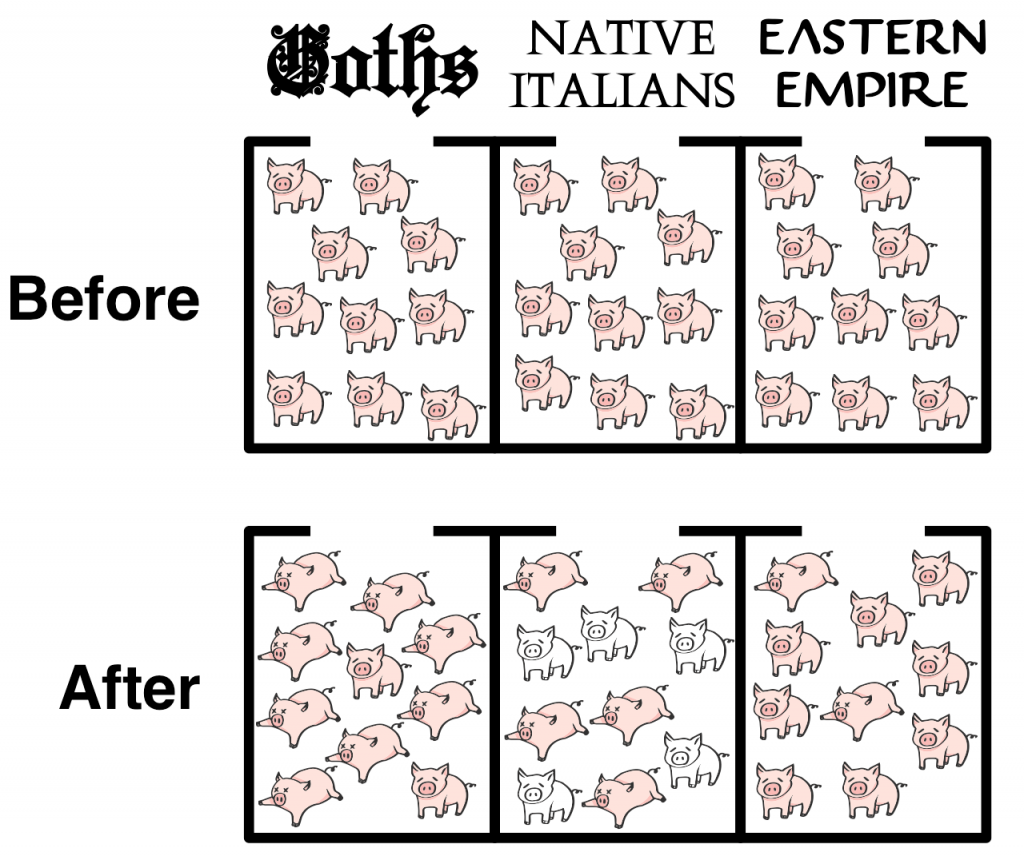
To make a decision whether he should fight Belisarius and try to lift the siege of Naples, Theodatus asked a Hebrew fortuneteller as to the likely outcome of the conflict. The fortuneteller told him to place 3 groups of 10 pigs each (presumably randomly selected) in separate huts, label them as Goths, Italians and East Roman soldiers, then wait a specified (but unstated) number of days. After doing just that, Theodatus and the fortuneteller entered the huts and noted that only 2 pigs labeled as Goths had survived, whereas most of the pigs labeled as East Roman soldiers lived. Of the pigs representing native Italians, half survived but had lost all of their hair. Theodatus interpreted the results to mean that the Italians would lose half of the population and all of their possessions, and that the Goths would be defeated, at little cost to the victorious Eastern Romans. Hence his reluctance to confront Belisarius at Naples.

In any event, Theodatus did not intervene and Belisarius ended up capturing both Naples and Rome from the Goths before being recalled by the Emperor. Losing both of these cities without much of a fight led the Goths to open rebellion and replace Theodatus as king of the Goths. Their chosen successor, Vittigis ordered the fleeing Theodatus to be apprehended and Theodatus perished at the hands of his pursuers.

Here is the original text (from the beginning of book 9, translated):

So the besieged, without the knowledge of the enemy, sent to Theodatus in Rome begging him to come to their help with all speed. But Theodatus was not making the least preparation for war, being by nature unmanly, as has been said before.[36] And they say that something else happened to him, which terrified him exceedingly and reduced him to still greater anxiety. I, for my part, do not credit this report, but even so it shall be told. Theodatus even before this time had been prone to make enquiries of those who professed to foretell the future, and on the present occasion he was at a loss what to do in the situation which confronted him—a state which more than anything else is accustomed to drive men to seek prophecies; so he enquired of one of the Hebrews, who had a great reputation for prophecy, what sort of an outcome the present war would have. The Hebrew commanded him to confine three groups of ten swine each in three huts, and after giving them respectively the names of Goths, Romans, and the soldiers of the [85]emperor, to wait quietly for a certain number of days. And Theodatus did as he was told. And when the appointed day had come, they both went into the huts and looked at the swine; and they found that of those which had been given the name of Goths all save two were dead, whereas all except a few were living of those which had received the name of the emperor’s soldiers; and as for those which had been called Romans, it so happened that, although the hair of all of them had fallen out, yet about half of them survived. When Theodatus beheld this and divined the outcome of the war, a great fear, they say, came upon him, since he knew well that it would certainly be the fate of the Romans to die to half their number and be deprived of their possessions, but that the Goths would be defeated and their race reduced to a few, and that to the emperor would come, with the loss of but a few of his soldiers, the victory in the war. And for this reason, they say, Theodatus felt no impulse to enter into a struggle with Belisarius. As for this story, then, let each one express his views according to the belief or disbelief which he feels regarding it.